With very little effort you can learn to use your calculator to calculate a number of important two-variable statistics.

• Enter bivariate data points into your calculator.
• Enter frequency bivariate data into your calculator.
• Calculate the slope of a straight line.
• Calculate the intercept of a straight line.
• Calculate the Pearson Product Moment Correlation Coefficient for a set of data.
• Compute the linear regression line for a set of data.
• Compute the mean and standard deviation for each to the two variables.
• Predict the value of one variable given the value of the other variable.

The statistical functions of your calculator can save you from doing days and days of monotonous, repetitious busy work.

Please have your calculator with you as you work through this lesson.

Notice that above the [DRG] button it says "MODE" in yellow. Your calculator is always in one of three modes: normal, one-variable statistics, or two-variable statistics. Press [2ndF] [DRG] and your calculator will ask if you want mode 0, mode 1, or mode 2. Press [2]. Notice that now your calculator screen has a black rectangle with the "STAT" written in light gray in the rectangle. That rectangle tells you that your calculator is in one of the two statistical modes (either one-variable or two-variable). The absence of that rectangle tells you that you are in normal mode. We will use the two-variable statistical mode (mode 2) for this lesson.

This section assumes your calculator is in xy mode. Before we begin, I want you to locate a few keys on your calculator. The data entry key [M+] is the button just above the [ )] button. The [STO] button is just to the left of the [M+] button. And, the recall button [RCL] is just to the left of the [STO] button.

It is also important that you do not confuse the negative button [+/-] with the subtraction button. The negative button [+/-], just below the [3] button, is used to enter negative numbers. The subtraction button [–], just above the [=] button, is not used for data entry.

The basic unit in bivariate algebra, bivariate geometry, and bivariate statistics is a "point." A point is specified by two variables, an x-value and a y-value. Points are written in the form of (x, y). For example, (23, -6) is a point with an x-value of 23 and a y-value of -6. And, the point (35, 3) has an x-value of 35 and a y-value of 3. Let's turn on our calculator, put it in xy mode, clear the statistical memories, and enter these two points: (23, -6) and (35, 3).
Press [ON]
[2ndF] [DRG] [2] to put your calculator in the Stat xy mode
[2ndF] [DEL] to clear your statistical memory.
Your screen will show Stat xy. Don't worry, this will disappear when we start entering data. Let's enter that data now:
[2] [3] [STO] [+/-] [6] [M+] entered the first point.
[3] [5] [STO] [3] [M+] entered the second point.

That's it!! Wasn't that easy? We only need to enter the data once, and as long as we do not clear our calculator, we can ask our calculator to compute a number of different statistics (or parameters) based on that data.

When given two different points, one, and only one, straight line can be drawn through those two points. Lines are specified with the equation y = a + bx where the value for a and/or b varies from line-to-line. Once a and b have been specified, the line has been specified.

Once your data has been entered, as ours has been, to obtain the value for a in the linear equation press [RCL] [(] Your display should read -23.25. Note the small blue A above the [(] button.

To obtain the b value, press [RCL] [)] Your display should read 0.75. Note the small blue B above the [)] button.

The equation for the line that goes through the two points (23, -6) and (35, 3) is y = -23.25 + 0.75x.

The equation for our line is y = -23.25 + 0.75x. If you specify any x and then solve this equation for y, the point specified with this x, y pair fall on the line. For example, if we specify x as 1, we can solve for y: y = -23.25 + 0.75(1) = -23.25 + 0.75 = -22.5. Therefore, the point (1, -22.5) falls on this line.

This is far more easily done with our calculator. We have already entered our two points. To find the y value that goes with 1, we just press
[1] to specify the x value, then
[2ndF] [)] our display should read -22.5. Notice the golden y' (y-prime) written above the subtraction key. This symbol represents the estimated y value.

Instead of specifying x and solving for y, we could specify y and solve for x. For example, we could specify the y in our linear equation of y = -23.25 + 0.75x to be 1 and solve for x:
1 = -23.25 + 0.75x which, by adding 23.25 to both sides becomes 24.25 = 0.75x which leads to 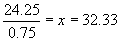. This means that (32.33, 1) also falls on our line. Or, we could just use our calculator. We just press
[1] to specify the y value, then
[2ndF] [(] our display should read 32.33333333. Notice the golden x' (x-prime) written above the addition key. This symbol represents the estimated x value.

One of the things that we will learn in the Measurements of Association portion of this course is how to find the line that best fits numerous data points. And, then, to describe how well that line fits our data points. Let's enter the following data points into our calculator: (-12, -4) (- 6, -3) (-2, -1) (1, 1) (3, 5) and (4, 7)
Press [ON]
[2ndF] [DRG] [2] to put your calculator in Stat xy mode
[2ndF] [DEL] to clear your statistical memory.

To find the linear equation for the best fitting line through this data, we must find a and b.
Press [RCL] [(]. Your display should read 2.14516129 which is the value of a,

To obtain the b value, press [RCL] [)]. Your display should read 0.655913978

The linear equation for the best fitting line (called the regression line) to the data we entered is:

y = 2.15 + 0.66x

Another statistic that you will learn about, the Pearson Product Moment Correlation Coefficient, tells us how well the line fits the data. The symbol for the Pearson Product Moment Correlation Coefficient is r. To find the r for our data, press:
[RCL] [÷] your display should read 0.909056586. Again, please notice the blue r above the [÷] button.

Again, let's look at the data points we entered: (-12, -4) (- 6, -3) (-2, -1) (1, 1) (3, 5) and (4, 7)

Notice that we have six points with six x-values (-12, - 6, -2, 1, 3, and 4) and six y values (-4 , -3, -1, 1, 5, and 7).

We can find the mean and standard deviations for the x variable the same way we did when we had only one variable. To find the mean of the x-values press:
[RCL] [4] your display should read -2

Before calculating the standard deviation and variance, you should determine if your data constitutes the entire population or just a sample of a population.

If you have the data for only a sample:

To find the sample standard deviation for the x values, press

[RCL] [5] your display should read 6.099180273

If you have the data for the entire population:

To find the population standard deviation for the x values, press

[RCL] [6] your display should read 5.567764363

Notice that these buttons [4], [5], and [6] are all in the same row. To find the mean and standard deviations for the y data, we move up a row to the [7], [8], and [9].

To find the mean of the y-values press:
[RCL] [7] your display should read 0.833333333

To find the sample standard deviation for the y values, press

[RCL] [8] your display should read 4.400757511.

To find the population standard deviation for the y values, press

[RCL] [9] your display should read 4.017323598

If your display did not show the numbers above, you probably pushed the [2ndF] [DEL] buttons when you should not have. When you press the [2ndF] [DEL] buttons, or change the mode, you clear out your data and need to re-enter all the data again before computing another answer based on that data. Moral to the story: Do not press the clear buttons unless you are entering a new data set.

1. What is linear equation for the line that goes through (3, -21) and (7, -15)?

Top