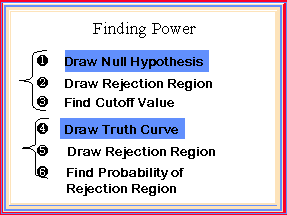
The steps for solving a power problem are:

First we draw the null hypothesis and draw the null hypothesis on it.
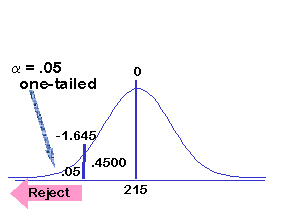
Then we use the z-score to find the cut off value.
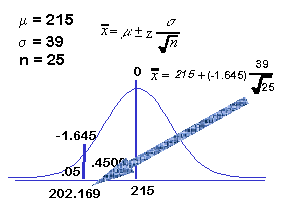
Now we draw the Truth Curve. If before treatment, the mean was 215. And, if our treatment reduces depression scores by 10, the new population mean should be 205 for people receiving our treatment.
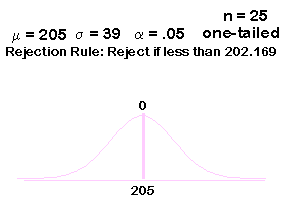
Our cut-off value we just calculated is 202.169. We add this to our truth curve:
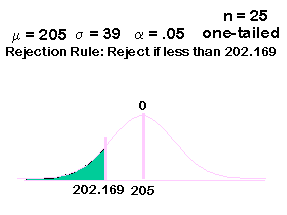
Now we calculate the new z-score for the cut-off value.
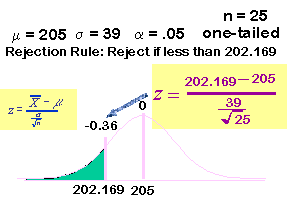
We look up this z-score in our z-table to find the value in the tail and we have an answer.
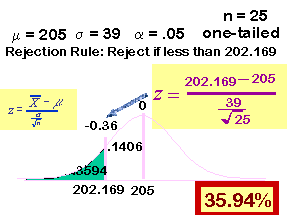
This means that even if the treatment does work by reducing depression by 10 points, we would only discover this treatment success 36% of the time. This means that, by using only 25 subjects, we would fail to find a significant difference 64% of the time even though the treatment really does work. Now to the next part of the problem.