This tutorial assumes you have already downloaded and installed the academic version of Statlets. If not, please press the [Links] button, go to Statlets web site and download and install it on your computer.

How to Do the Calculations for Correlations and Simple Linear Regression Using Statlet

 

For this tutorial, assume you teach in the Nursing department of a highly prestigious University. The department has developed a system of determining the hardiness of student applicants. Hardiness scores are rated from 0 to 1, with 1 being the most hardy. You take a random sample of students who have completed their first year of nursing education and compare their hardiness score with their grade point average for the first year. Is there a linear relationship between the hardiness score and the GPA of nursing students? What is the linear equation you would use to predict a student's first year GPA from that student's hardiness score? What GPA would you predict for a student whose hardiness score is .72?

 

1. When you start Statlets, the following spreadsheet should appear. If not, click on the "File" pull down window and select "New."

 

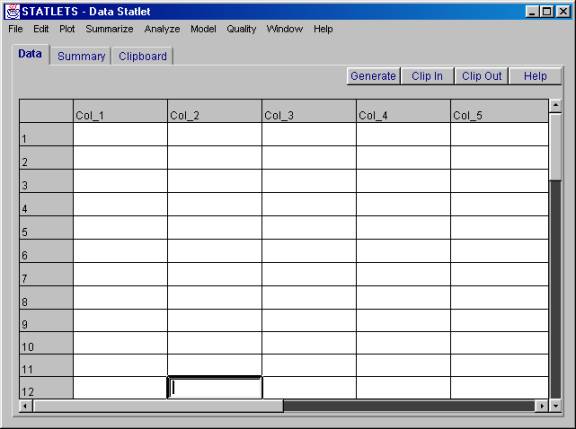
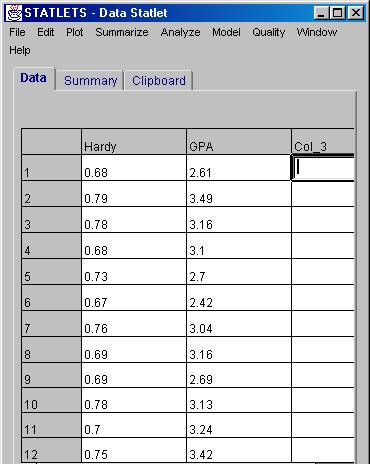
2. Name "Col_1" "Hardy" and enter the following data in that column:

Hardy
  .68
  .79
  .78
  .68
  .73
  .67
  .76
  .69
  .69
  .78
  .70
  .75
  .68
  .69
  .78

3. Name "Col_2" "GPA" and enter the following data in that column:

GPA
2.61
3.49
3.16
3.10
2.70
2.42
3.04
3.16
2.69
3.13
3.24
3.42
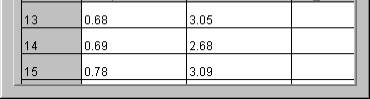
3.05
2.68
3.09

4. Click on the "Model" menu, slide down to "Regression Analysis" and slip over to "Simple Regression."

 

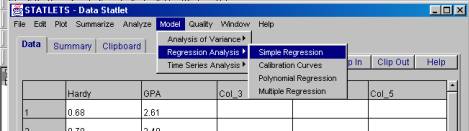
the following dialog box will appear:

5. Select "GPA" as the dependent variable (the variable we hope to predict) and "Hardy" as the independent variable.

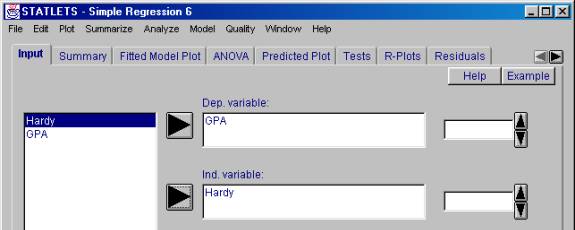
6. Wow!! That was tough. I'm almost in a sweat. But we are done. Now all that is left is reading the results. To see the results, click on the "Summary" tab.

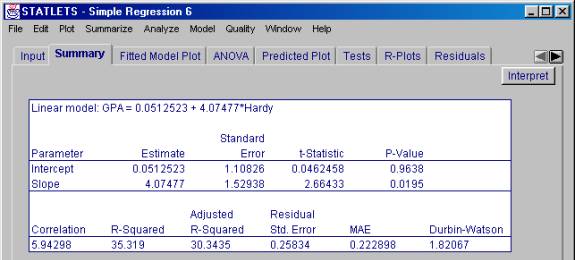
From this output, we would make the following decision and conclusion:

Decision: Reject H₀

Conclusion: At an alpha level of .05, there is significant direct relationship between hardiness and first year grade point average, r(13) = .59, p = .0195. The variation in hardiness accounts for 35.319% of the variance in GPA. The linear equation for predicting GPA from hardiness is: GPA = 0.0513 + 4.0748*Hardiness.

The only peculiar thing is that the Correlation shown in the table has its decimal moved one to the right. The r of .594298 is reported as 5.94298. It is not worth the time to explain why the author of this program chose to do this, but realize that he did.

7. To predict the GPA for a student with a hardiness score of .72 select the "Predictions" tab - you probably need click on the right facing arrowhead  on the right side of the tabs.

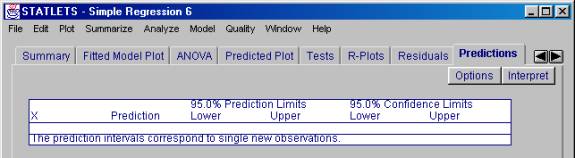
8. Click on the [Options] button.

9. Enter .72 under the X:

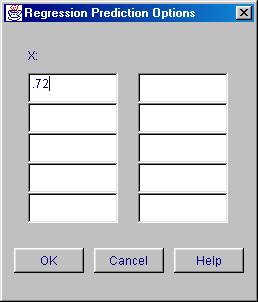
10. Click on the [OK] button.

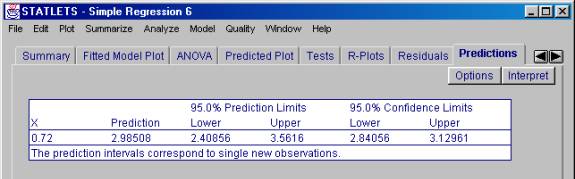
We would predict a student with a hardiness score of .72 to earn a first year GPA of 2.98508 and we are 95% confident that the GPA will be between 2.84056 and 3.12961.

By the way, I just looked up your hardiness score. Your hardiness score was .99, so I expect you to ace statistics.