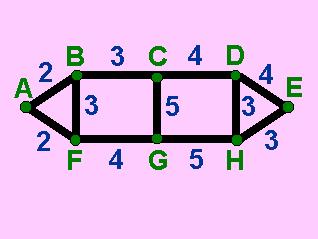
Questions 10-13 all refer to the following graph, which has costs associated with each edge:

c. 15
Nope,
as the two graphs below show, there are only two different ways we can create paths that have cost of 17 or less (which is more generous than 15) without forming a cycle. In the first graph, every vertex is visited but there are two paths instead of just the one required for a tree. The second graph has just the one path (as required for a tree) but does not visit every vertex which would be required for a spanning tree.
